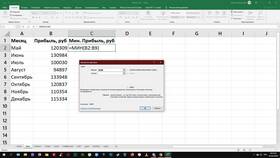
В математических и научных формулах символ суммы (Σ) представляет собой операцию сложения последовательности чисел или выражений. Это компактный способ записи сложения большого количества слагаемых.
Содержание
Математическое определение суммы
Сумма в формуле обычно записывается с использованием символа сигма (Σ) и включает три основных компонента:
- Нижний индекс - начальное значение переменной суммирования
- Верхний индекс - конечное значение переменной суммирования
- Выражение для суммирования - формула, зависящая от переменной суммирования
Примеры записи сумм в формулах
| Формула | Развернутая запись |
| Σni=1 i | 1 + 2 + 3 + ... + n |
| Σ5k=2 k2 | 22 + 32 + 42 + 52 |
| Σ∞n=0 xn/n! | 1 + x + x2/2! + x3/3! + ... |
Области применения сумм в формулах
Основные применения:
- Арифметические и геометрические прогрессии
- Теория вероятностей и статистика
- Физические расчеты (механика, термодинамика)
- Экономические модели
- Компьютерные алгоритмы
Свойства сумм в формулах
| Свойство | Формульная запись |
| Линейность | Σ(ai + bi) = Σai + Σbi |
| Вынос константы | Σ(c·ai) = c·Σai |
| Разбиение суммы | Σni=1 = Σki=1 + Σni=k+1 |
Как читать формулы с суммой
- Определите переменную суммирования (индекс)
- Найдите начальное и конечное значения индекса
- Подставьте последовательно все значения индекса в выражение
- Сложите все полученные значения
Особые случаи суммирования
- Бесконечные суммы (ряды) - требуют проверки сходимости
- Кратные суммы - суммирование по нескольким индексам
- Условные суммы - с дополнительными ограничениями на индекс
- Взвешенные суммы - с коэффициентами перед слагаемыми
Практическое значение
Использование символа суммы в формулах позволяет:
- Компактно записывать сложные выражения
- Упрощать математические выкладки
- Унифицировать запись алгоритмов
- Обобщать конкретные случаи сложения
Понимание работы с суммами в формулах является важным навыком для работы в точных науках и позволяет эффективно решать широкий круг математических задач.