Средняя линия трапеции - это отрезок, соединяющий середины боковых сторон данной геометрической фигуры. В отличие от суммы средней линии, которая сама по себе не является математическим термином, важное значение имеет длина средней линии трапеции.
Содержание
Основное свойство средней линии трапеции
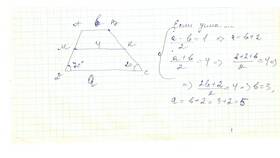
Длина средней линии трапеции равна полусумме длин её оснований. Это ключевое свойство, которое часто используется при решении геометрических задач.
Формула для расчета длины средней линии
Формула вычисления длины средней линии (m) трапеции с основаниями a и b:
| Формула | m = (a + b) / 2 |
| Где: |
|
Примеры расчета
- Для трапеции с основаниями 8 см и 4 см:
m = (8 + 4) / 2 = 6 см
- Для трапеции с основаниями 10 м и 6 м:
m = (10 + 6) / 2 = 8 м
Дополнительные свойства средней линии
- Средняя линия параллельна основаниям трапеции
- Средняя линия делит высоту трапеции пополам
- Отрезок, проходящий через точку пересечения диагоналей параллельно основаниям, равен половине средней линии
Доказательство свойства средней линии
Рассмотрим трапецию ABCD с основаниями AD и BC. Пусть M - середина AB, N - середина CD. Проведём диагональ AC, которая пересекает MN в точке K. Треугольники AMK и ABC подобны, поэтому MK = BC/2. Аналогично KN = AD/2. Следовательно, MN = MK + KN = (BC + AD)/2.
Применение в задачах
Знание свойства средней линии трапеции позволяет:
- Находить неизвестные длины оснований
- Решать задачи на вычисление площади
- Определять параметры сложных геометрических фигур
- Упрощать доказательства теорем